男生洗澡很久不出来会在干什么呢？

如果是浴缸的话，就是一直在那泡着，泡到水冷了，手皱皮了。

如果是淋浴的话，就一直冲，冲到没水了，水冷了。

就这。

事实上很多时候男人去洗澡与其说是洗澡，不如说是泡澡，什么都不做，泡半天，泡的暖洋洋头晕晕的，这挺舒服的。

很多时候洗澡，清洁是次要的，暖身放松才是最重要的。

在很多时候只要条件允许，男生洗澡的时间绝对不是女生能赶上的。

男生是可以在浴缸里什么都不做睡到冻醒的。

在农村，小孩子夏天都喜欢下水，我们叫洗冷浴，不仅仅是因为水冷，就是泡在水里很舒服，感觉很奇特。

人有一种奇怪的漂浮虚空感。放空思绪。

记得上高中的时候第一次学瞬时变化率和导数的那天感觉整个世界都变了，从学校走回家不管看到什么现象都要去联想一下微积分。

那天晚上洗完澡之后关上淋浴，穿上睡衣刚开始刷牙突然听到“滴”的一声。 转头一看是花洒里的水滴到地上的声音。 回过头去继续刷牙，“滴”，又落下来一滴。

走火入魔的我又开始想了，“地上的现有水量是函数f，f现在的导数是正的。”

“滴”，第三滴水滴下来的时候我发现事情并没有那么简单。

诶这花洒每次滴下来的时间间隔好像越来越长了啊？

这说明...啊f的导数是正的，但是导数的导数是负的。

我为自己的发现感到骄傲，不过另外一个疑惑接踵而至。

那导数的导数的导数呢？

导数的导数的导数的导数呢？

导数的导数的导数的导数的导数呢？

为了解决这些世界性难题，接着我在浴室里的马桶上坐了二十分钟，看着花洒把水滴完了， 然而还是没有总结出任何规律。

这就是我在浴室呆得最久的一次。

还好几个月之后学了微分方程才让我彻底想通了这个淋浴难题，避免了以后发生更多的类似事件。

更搞笑的是，几年之后一个数学教授在和我们讲极限的时候，也拿他洗澡调水温的经历当例子... 他说他一定要洗42度水，但是那个调温的转子坏了没办法调42，于是他就从41度无限的靠近42，虽然不能等于42但是他已经感受不到差别了。

我当时就在寻思了，原来大家对微积分的领悟都是在浴室进行的啊。

更新一下：

评论区有同学问道“那你后来是怎么想通的？”

我稍微讲一下我后续的一些理解吧，我只能从数学上解释，物理上我是不太懂。

设地上的水量y是t的一个函数，f(t)。

水龙头关上之后，水管里还可以滴出来的水是一个常数量，那么f(t)存在一个上限A（滴水之前已经有的量加上水管里的量）,可以理解为时间足够长之后管子里的水全部从花洒里滴在地上，一共就只能有A那么多的量。

我们知道水管里的水越多，那么水滴落下来的时候就会越快，水管里的水越少，水滴下来的速度就越慢。 物理上的解释也许是因为水多的时候压力比较大？

在地上的水f(t）的角度上来讲，也就是说现有的水量和A的差距越大（意味着还有很多没滴下来），f(t)的增加速度就越快；现有水量和A的差距越小（意味着大部分已经滴完了），f(t)的增加速度就越慢。这模型也符合我们平时的观察 ，一开始滴得很快，最后几滴水是滴得非常慢的。

总结起来就是：f '(t) 和A与f(t)的差成正比。

dy/dt = k[A-f(t)]

很容易可以解出

其中A是水管里的水，也就是f(t)的上限，A-C是刚开始地上已有的水量（当t=0的时候f(0)=A-C），k是个比例系数。

这个函数的图长这样

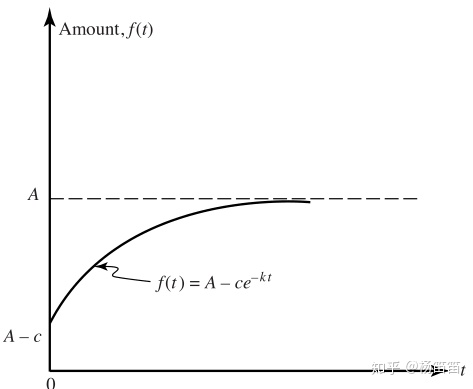
f(t)一直在增长，这也和我当时的f导数为正的观察相符。

f(t)增长得越来越慢，或者说f(t)是concave down,这也和我当时“滴水间隔越来越长”的观察相符。

这个模型叫作restricted growth，它的应用也非常广泛，比如Newton's Cooling Law牛顿冷却定理也指出物体和周围温差越大降温速度就越快。感兴趣的同学可以去查一下资料。